How triangles revolutionized mapmaking
And more lessons from Ian Stewart's In Pursuit of the Unknown: 17 Equations That Changed the World


Equations are the lifeblood of mathematics, science, and technology. Without them, our world would not exist in its present form. However, equations have a reputation for being scary: Stephen Hawking's publishers told him that every equation would halve the sales of A Brief History of Time. [In Pursuit of the Unknown: 17 Equations That Changed the World]
This captures our aversion to equations well. Yet, as mathematician Ian Stewart argues in his book In Pursuit of the Unknown: 17 Equations That Changed the World, "[e]quations are too important to be hidden away."
Equations are a vital part of this world. And you don't need to be a rocket scientist to appreciate them.
The Week
Escape your echo chamber. Get the facts behind the news, plus analysis from multiple perspectives.

Sign up for The Week's Free Newsletters
From our morning news briefing to a weekly Good News Newsletter, get the best of The Week delivered directly to your inbox.
From our morning news briefing to a weekly Good News Newsletter, get the best of The Week delivered directly to your inbox.
There are two kinds of equations in mathematics. Stewart writes:
One kind presents relations between various mathematical quantities: the task is to prove the equation is true. The other kind provides information about an unknown quantity, and the mathematician's task is to solve it — to make the unknown known. The distinction is not clear-cut, because sometimes the same equation can be used in both ways, but it's a useful guideline. [In Pursuit of the Unknown: 17 Equations That Changed the World]
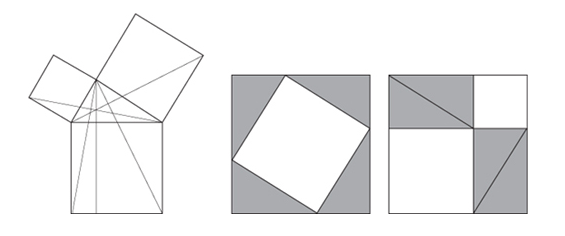
An example of the first kind of equation is Pythagoras' theorem, which is "an equation expressed in the language of geometry." If you accepts Euclid's basic geometric assumptions, then Pythagoras' theorem must be true.
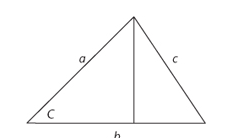
In the famous translation by Sir Thomas Heath, proposition 47 (Pythagoras' theorem) of Book I reads:
A free daily email with the biggest news stories of the day – and the best features from TheWeek.com
In right-angled triangles the square on the side subtending the right angle is equal to the squares on the sides containing the right angle.
Many triangles in real life are not right angled. But this does not limit the use of the equation a² + b² = c² because any triangle can be cut into two right-angled ones.
A good example of the second kind of equation is Newton's law of gravity. "It tells us how the attractive force between two bodies depends on their masses," Stewart writes, "and how far apart they are. Solving the resulting equations tells us how the planets orbit the Sun, or how to design a trajectory for a space probe." This isn't a mathematical theorem. Rather, it's true for physical reasons and fits our observations.
Equations, as simple as they appear, have redirected human history time and time again. "An equation derives its power from a simple source," Stewart writes. "It tells us that two calculations, which appear different, have the same answer."
The power of equations lies in the philosophically difficult correspondence between mathematics, a collective creation of human minds, and an external physical reality. Equations model deep patterns in the outside world. By learning to value equations, and to read the stories they tell, we can uncover vital features of the world around us. [In Pursuit of the Unknown: 17 Equations That Changed the World]
Pythagoras' theorem
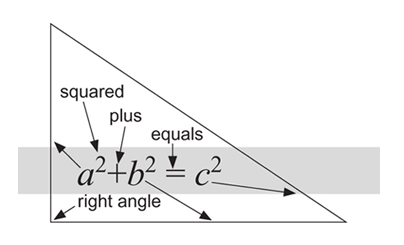
This is the first equation presented in the book. As Stewart writes, it is not only "a vital link between geometry and algebra, allowing us to calculate distances in terms of coordinates. It also inspired trigonometry." What else did it inspire? "Surveying, navigation, and more recently special and general relativity — the best current theories of space, time, and gravity."
Think about it this way: Triangulation is an indirect way of determining distance by employing angles. Here's Stewart:
When surveying a stretch of land, be it a building site or a country, the main practical consideration is that it is much easier to measure angles than it is to measure distances. Triangulation lets us measure a few distances and lots of angles; then everything else follows from the trigonometric equations. The method begins by setting out one line between two points, called the baseline, and measuring its length directly to very high accuracy. Then we choose a prominent point in the landscape that is visible from both ends of the baseline, and measure the angle from the baseline to that point, at both ends of the baseline. Now we have a triangle, and we know one side of it and two angles, which fix its shape and size. We can then use trigonometry to work out the other two sides.
In effect, we now have two more baselines: the newly calculated sides of the triangle. From those, we can measure angles to other, more distant points. Continue this process to create a network of triangles that covers the area being surveyed. Within each triangle, observe the angles to all noteworthy features — church towers, crossroads, and so on. The same trigonometric trick pinpoints their precise locations. As a final twist, the accuracy of the entire survey can be checked by measuring one of the final sides directly. [In Pursuit of the Unknown: 17 Equations That Changed the World]
Surveys routinely employed triangulation by the late 18th century. And while we don't explicitly use it today, it is still there in how we deduce locations from satellite data.
In Pursuit of the Unknown: 17 Equations That Changed the World is an elegant argument for why equations matter.
More from Farnam Street...
- Socrates and the search for wisdom
- Leonard Mlodinow: The laws of truths and half truths
- Genevieve Bell on the value of humanities in an executive roll
Farnam Street also feeds your brain every Sunday with Brain Food. Join 34,000 other smart people and read what you've been missing.
Shane Parrish is a Canadian writer, blogger, and coffee lover living in Ottawa, Ontario. He is known for his blog, Farnam Street, which features writing on decision making, culture, and other subjects.
-
 Political cartoons for January 11
Political cartoons for January 11Cartoons Sunday’s political cartoons include green energy, a simple plan, and more
-
 The launch of the world’s first weight-loss pill
The launch of the world’s first weight-loss pillSpeed Read Novo Nordisk and Eli Lilly have been racing to release the first GLP-1 pill
-
 Maduro’s capture: two hours that shook the world
Maduro’s capture: two hours that shook the worldTalking Point Evoking memories of the US assault on Panama in 1989, the manoeuvre is being described as the fastest regime change in history